Let’s say I offered you $100 now or $100 in 10 years. Which option would you choose? Probably the $100 now, because money now is better than money in the future. But what if I offered you $100 now or $150 in 10 years? Assuming you don’t have an immediate need for the money, you would like to know which one is worth more. For that, you need to the determine how much the future $150 are worth now. In other words, you need to calculate the present value of $150.
To determine the present value of a future amount, you need two values: interest rate and duration. The interest rate determines how quickly a present amount grows over time, and the duration determines how much time the mount has to grow. Usually the duration is known, but the interest rate depends on a judgement call. For example, if the amount in question is an asset that has to be divided in a divorce case.
Profitable Benefits of Legal Project Management
LPM has a proven track record of improving efficiency, increasing profits, and strengthening relationships between your firm and its clients.
The formula to calculate the present value is:
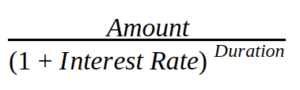
Let’s break it down:
- Start with your interest rate, expressed as a fraction. So 5% is 0.05.
- Add 1 to the interest rate.
- Raise the result to the power of duration.
- Divide the amount by the result.
For example, let’s take the following input:
Amount = $150
Interest Rate = 5% per year
Duration = 10 years
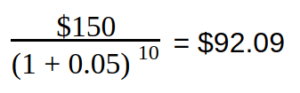
Note that the values have to use the same units, or else they need to be adjusted. For example, if you use an annual interest rate, your duration should be in years as well, and we assume that the interest compounds once per period.
Assuming 5% interest rate, it is better to take $100 now than $150 in 10 years, because the present value of $150 is only $92.09. But if the interest rate was lower than 4.13%, it would have been better to wait for 10 years, because at that rate, the present value would be about $100.
If you are looking for an application that provides this type of calculation and much more, check out Math4Law, a new web service that brings the power of Math to Law Offices. Calculating interest on unpaid arrears has never been easier!